The approach proceeds by first predicting the overall surface of the region area at instant . This consists in the forecasting of the value of the total surface by applying a sort of linear regression adapted to the problem over the analytical data. Since many of the changes which occur are directional and occur incrementally over long periods of time, some areas will be more influenced by these changes. Thus, there will be zones of the region area which will present a growth (progression) and other zones will be under regression.

The next step generates maps which represent progression and regression zones between two instants of time, and . These areas are obtained by the overlay of different thematic maps followed by an image differencing (subtraction between the two images overlayed). In this way for n instants, we will have n-1 maps of progression and n-1 maps of regression.

This approach is based on the principle that an area of closest proximity to a progression zone will trend to the growth rather than an area close to a regression zone and vice versa. Thus the distance between any point and a region of progression or regression is an information that should be considered in order to determine the propensity of this point to the growth or regression. For every pixel of the image we calculate a coefficient of the pixel.

In order to calculate the coefficient of evolution for each pixel, all maps of progression and regression obtained are required. Naturally the more recent the maps are, greater are their influence on the results. In this way, time is also an important information which can be represented as a temporal distance [9]. Since time is one-dimensional, the temporal distance may represent the length of interval between any two given locations in time.

Even the surfaces of the progression and regression zones should be considered in the calculus because it is very likely that a pixel in the middle of a progression zone and a regression zone will be heavily influenced by the zone with the greater surface. In this way for each pixel of the image we determine two values: the first provides the tendency of the pixel for progressing and the second provides its tendency for regression.

Let

• p be the number of regions of progress and n be the number of geographic maps (for n instants),
• Dk be the distance between the pixel (i,j) and the region k,
• Sk be the surface of the region k and
• Tt be the temporal distance between the year to predict and the year of the map being analyzed.

The coefficient of evolution is defined by:

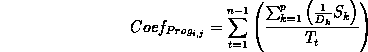Analogously, the coefficient of regression of each pixel is given by:

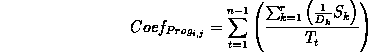where r is the number of zones of regression.

The coefficient of evolution is the result of a subtraction between the coefficients of progression and regression previously calculated:

After the calculus, the table of coefficients will be normalized in such a way that the coefficient of evolution for each pixel of the image is determined by

• a membership function based on the time,
• the pixel location with regard to progression and regression zones and
• the surface of these zones.

In this way, the most favorable zones to progress are affected by a strong coefficient and the zones which are less affected by a weak coefficient. The purpose is to obtain a unique coefficient for every pixel. This coefficient provides a belonging degree of the pixel to the progression.