The first step consists in calculating the weights of the layer of output C. For the neurons of layer C,

noted N_{C, I}   , the adjustment of the weights w_{j, I} is given by:

with

 With      and    .

For the hidden layer, the error is set from the sum of errors computed on each neuron of the following layer, depending on their connected weight. For the neurons N_{L, I} of the layer L, the expression is given by:

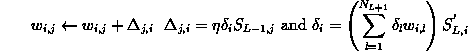with and

As using the rule, the process is applied until the total error is lower than a preset threshold. The expression of the error for a network with N outputs to which K is presented is:

The method of backpropagation can be a heavy process if the number of neurons is significant. The learning time may be very long. The adjustment of the learning coefficient allows convergence to be accelerated, but a significant value can generate oscillations and disable the convergence.

The choice of a network topology to obtain the best results is rather delicate. It is necessary to choose the simplest network performing the shortest processing time, but also a sufficiently complex topology to distinguish all the classes without confusion.