
Example

Suppose that a source s must assess with what degree it
is possible, in its opinion, that a pixel belongs to a set of three classes.
Let
- ds1(x)
= 0.7 the degree allotted to class 1,
- ds2(x)
= 0.3 the degree allotted to class 2,
- ds3(x)
= 0.5 the degree allotted to class 3.
We get 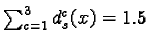 .
.
- First, we assign the masses of evidence msc
so that their sum equals 1, and so
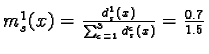 ,
,
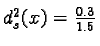 ,
et
,
et 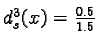 .
.
- We must now determine what is the uncertainty
of this source s about the choice of the class to
which pixel x belongs.
[Zahzah, 1992] proposed to evaluate
this uncertainty 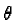 by the distance between the class which
is considered to be the most plausible for pixel x, and all
the other classes. This distance is likened to the degree of confusion
between the classes which are possible for this pixel.
by the distance between the class which
is considered to be the most plausible for pixel x, and all
the other classes. This distance is likened to the degree of confusion
between the classes which are possible for this pixel.
Two situations can be considered:
- 1.
- If the source indicates:
- one unique class c as totally
possible ( dsc(x)
= 1), and
- all the other classes impossible
(
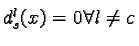 ),
),
then there is no confusion. The source came down clearly in favour of
a single class, and there is no uncertainty. In this case, uncertainty 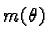 is set to 0 as the source is sure of its choice.
is set to 0 as the source is sure of its choice.
- 2.
- At the opposite, we can be in a situation of high
confusion. The source ignores which class must be given more
importance and then assigns close degrees(
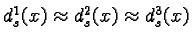 )
to each class. In this case, confusion is very high. To express this confusion,
a large part of the mass of evidence is assigned to
)
to each class. In this case, confusion is very high. To express this confusion,
a large part of the mass of evidence is assigned to 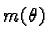 .
.





IRIT-UPS


![]()
![]()
![]() .
.
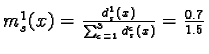 ,
,
![]() by the distance between the class which
is considered to be the most plausible for pixel x, and all
the other classes. This distance is likened to the degree of confusion
between the classes which are possible for this pixel.
by the distance between the class which
is considered to be the most plausible for pixel x, and all
the other classes. This distance is likened to the degree of confusion
between the classes which are possible for this pixel. ![]() is set to 0 as the source is sure of its choice.
is set to 0 as the source is sure of its choice.