Union of fuzzy subset: t-conorms

Union of Fuzzy Subset: T-Conorm

The union of two fuzzy sets A and B is associated to a map u:

$\begin{displaymath}u : [0,1] \times [0,1] \rightarrow [0,1]\end{displaymath}$

(27)

The argument of this map is the couple defined from the degrees of membership of element x to fuzzy sets A and B. It returns the degree of membership of the element considered to the set $A \cup B$ . So:

$\begin{displaymath}\forall x \in \Omega, \quad u[\mu_A(x), \mu_B(x)] = \mu_{A \cup B}(x)\end{displaymath}$

(28)

Map u must satisfy several properties to be a T-conorm: $\forall a, b, c \in [0,1]$

axiom u₁: closure condition: u(a,0) = a;
axiom u₂: monotonicity: $b \leqslant c \Rightarrow u(a,b) \leqslant u(a,c)$ ;
axiom u₃: commutativity: u(a,b) = u(b,a);
axiom u₄: associativity: u(a, u(b,c)) = u(u(a,b), c).

Comparing conditions u₁-u₄ to conditions i₁-i₄, it can be seen that only the boundary condition is different. The justification of these conditions is similar to the justification of t-norms.

The main additional conditions required for the fuzzy unions are described by the following axioms:

axiom u₅: u is a continuous function;
axiom u₆: sub-idempotency: u(a,a) > a;
axiom u₇: strict monotonicity: a₁ < a₂ and $b_1 < b_2 \Rightarrow u(a_1,b_1) < u(a_2,b_2)$ .

These axioms are also similar to i₅-i₇ (fuzzy intersection) but the over-idempotency condition of fuzzy intersections has been replaced by sub-idempotency condition. The most usual t-conorms are the following: $\forall a,b \in [0,1]$

- standard union:	$u(a,b) = \max(a,b)$ ;
- algebraic sum:	$u(a,b) = a + b - a \cdot b$ ;
- boundary sum:	$u(a,b) = \min(1, a+b)$ ;
- drastic union:	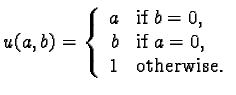$u(a,b) =\left\{ \begin{array}{rl}a & \mbox{if } b = 0, \\b & \mbox{if } a = 0, \\1 & \mbox{otherwise.}\end{array} \right.$

$\begin{displaymath}\forall a,b \in [0,1] \;\;\;\max(a,b) \leqslant a + b - a \......b\leqslant \min(1, a+b)\leqslant u_{\text{drastical}}(a,b)\end{displaymath}$

IRIT-UPS