Properties of -cuts

Properties of $\alpha$ -Cuts

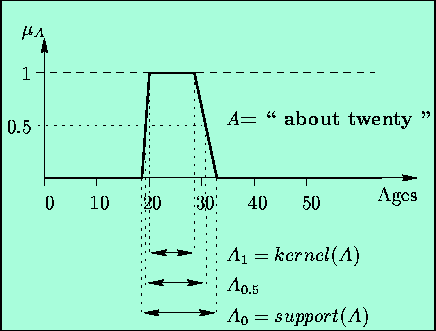
When we build an $\alpha$ -cut $A_\alpha$ of fuzzy subset A, we can say that $\alpha$ represents the threshold from which the concept of membership, although relative in the definition of A, is regarded as sufficient to build its approximate subset $A_\alpha$ .

The more demanding we are about the concept of membership, the more this threshold is raised, and the fewer elements of $\Omega$ satisfy the membership criteria. The $\alpha$ -cuts of A are nonfuzzy parts of $\Omega$ , encapsulated with respect to the value of $\alpha$ , i.e. if $\alpha^\prime \geqslant \alpha$ , then $A_{\alpha^\prime } \subseteq A_\alpha$ .

**Figure 23:** Example of $\alpha$ -cuts associated with fuzzy subset A.
$\begin{figure}\begin{center}\epsfbox{c2-alpha-coupe-eng.eps}\end{center}\end{figure}$

Operations on fuzzy sets are compatible with the classical operations of crisp sets.

Thus, for all A and B of $\mathcal{F}(\omega)$ and for all $\alpha$ of [0, 1], performing the fuzzy intersection or union of A and B, and then constructing $\alpha$ -cuts, is equivalent to seeking the $\alpha$ -cuts of A and B and then performing their classical intersection or union:

$(A \cap B)_\alpha = A_\alpha \cap B_\alpha$ ,
$(A \cup B)_\alpha = A_\alpha \cup B_\alpha$ ,
si $B \subseteq A$ alors $B_\alpha \subseteq A_\alpha$

If level $\alpha = 0$ is selected, then $A_\alpha = \Omega$ . If level $\alpha = 1$ is selected, then $A_\alpha$ is the kernel of A, which could be empty.

IRIT-UPS