Assume the following multiple propositions rule using the premises operator AND:

IF ( is ) and ...and ( is ) THEN Y is B.

The generalized modus ponens can be expressed by:

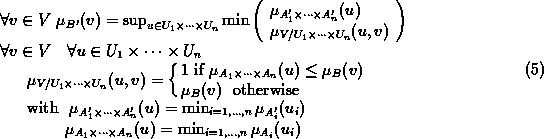However, the computation of the generalized modus ponens with formula 5 needs the evaluation of several Cartesian products and projections.

So, to reduce computing time and memory space, each n-multiple proposition rule is cut in n simple rules, and the generalized modus ponens can be applied on each simple rule to provide n fuzzy sets which are combined in a unique fuzzy set with an appropriate combination (depending on the premises operator AND, OR, AVG) as following :

Effectively, with the 2 following Brouwer-Gödel implication properties:

and

it is easy to show the equivalence between formula 5 and the rule cutting method for the operator AND and OR. However there is no equivalence with the operator AVG ( ), but it can be approximated.

Basically, combination operators can be separated in three families [1]:

• conjunctive,
• disjunctive and
• compromise

AVG is a compromise operator between conjunctive and disjunctive operators like . Experimental result shows hat the behaviour of the AVG operator is constant with such a computation.