The methods known as of " active contours " or ``Snakes'' [M. Kass, 1988a] model a mechanical behaviour. The initial curve becomes deformed gradually to follow the lineaments as well as possible.

The process is iterative and tries to optimize a function of energy. Energy is a function of the internal and external characteristics to the curve. The choice and the influence of the characteristics depend on the objects to detect. But to avoid divergences, it is imperative to use convex profiles, i.e. without noise, for the evaluation of external energy.

In practice, these methods are efficient when the deformations remain tiny, and often are only used to refine the matching process. Their nature, of mechanical origin, is used to force the shape of the curve. It is possible to control the flexibility of the curve and thus to adapt the parameters according to the type of object to be detected. This method constitutes a good way to convert a succession of pixels into vectors. Moreover, the adjustment of the parameters of flexibility makes it possible to take into account generalization desired to represent the objects.

A method proposed by [A. A. Amini, 1990] functions on the principle of dynamic programming while integrating mechanical qualities of the ``snake' '. The original curve consists of a succession of points more or less distant, and optimization is calculated in the neighbourhood of the points. The space of search can be more restricted than in the case of the dynamic programming, since it adapts dynamically in the neighbourhood of the ``snake' '. The extent of the neighbourhood makes it possible to get rid of the noise and to guarantee a better convergence. In return, execution time increases considerably. The process is iterative and converges towards the optimal solution by deformation of the curve.

In the example of figure 15, with a neighbourhood of dimension 3x3, the points are moved towards the curve represented in fine dotted lines. Points P_n-1 et P_n+1 converge at the current iteration, and P will converge at next iteration.

Figure 15: Convergence of ``Snake'' algorithm during an iteration.

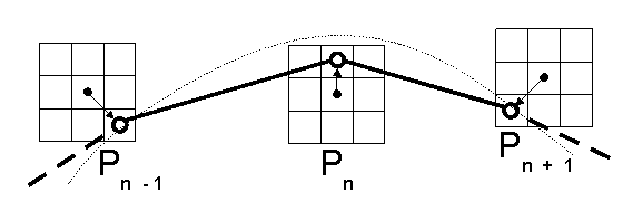In any point, energies are given by the sums of energies around the preceding point and energies around the current point. The minimal sum is retained as optimal value.

At the end of the iteration, points converge towards the positions which generated the optimal path. Energies around the current point integrate the internal mechanical constraints of the curve and the energies external to the curve in a way similar to the ``snakes' '. The criterion to be optimized in term of dynamic programming is the total energy of the curve, as for traditional ``snake'.

It should nevertheless be noted that the context of the lineament must be rather convex. Otherwise, it is necessary to use a significant neighbourhood for each point, and complexity increases so much that the operator takes most of the resources of the computer.

Some algorithms are able to ensure convergence in a non convex environment, but it is necessary to initialize the ``snake' ' in a configuration close to the optimal solution.