Presentation of the method

Presentation of the Method

During fusion of a great number of sources, it often happens that they do not all have a common interval, but a majority of them express such an interval, only some sources not agreeing with the majority. So, it is regrettable that adaptive fusion privileges the few sources having created the conflict causing disjunctive fusion whereas all the other sources fell into agreement.

It is clear that the true value of the parameter has much more chance of being in the intersection of distributions provided by a majority of agreeing sources than in the distribution provided by the few sources creating the conflict. Dubois and Prade proposed a method of fusion called quantified adaptive fusion, to correct the weakness of adaptive fusion when a great number of sources are to be fused.

It is assumed that the sources are in overall agreement (i.e. the majority of the sources to fuse agree). Conjunctive fusion is the method of fusion best suited to manage agreeing sources. But, it is necessary to determine which the agreeing sources are. Their number is computed from the degree of consensus h. It allows the set of reliable sources to be estimated both optimistically and pessimistically.

Let p be the total number of sources to fuse, J be any subset of sources, and $h(J) = \sup_{\omega \in \Omega}( \min_{i \in J}(\pi_i(\omega)) )$ be the degree of consensus of subset J of the sources.

Pessimistic estimation m and optimistic estimation n of the number of reliable sources ( $m \leqslant n$ ) are defined as follows:

$\displaystyle m = \max\{ \vert J\vert, h(J) = 1 \}$

(pessimistic operation)

(60)

$\displaystyle n = \max\{ \vert J\vert, h(J) > 0 \}$

(optimistic estimation)

(61)

It is plausible to assume that, among the p sources available, there is a group of at least m reliable sources, but never more than n. The previous adaptive rule is then generalized with p sources like this:

$\begin{displaymath}\forall \omega \in \Omega, \quad\pi_{\text{adq}}(\omega) =......ext{D}}{\underbrace{\min( 1-h(n), \pi_{(m)}(\omega))}} \right)\end{displaymath}$

(62)

With $h(n) = \max \{ h(J), \vert J\vert = n \}$ .

The rule of quantified adaptive fusion (62) consists of two parts:

Part C is used for renormalized conjunctive fusion of the subset of the sources in greatest agreement, even if h is slightly greater than zero, over the same range of possible values. It corresponds to the optimistic estimation n of the number of reliable sources.
Part D is used to express the interval not covered by part C. It is assumed to lead to fusion that is more ``disjunctive'' than part C (possibility distributions provided by each source). It corresponds to the pessimistic estimation m of the number of reliable sources.

The number of sources kept for fusion is even more restricted, than in part C. Conjunctive fusion is still the only type used for the few agreeing sources m. But, it should be noted that these sources can be very few, and thus the intersection intervals of the possibility distributions, provided by the small number of sources, have more chance of being numerous and vast than in part C. In this way part D can be performed rather as a ``disjunctive'' fusion.

In particular, if it is impossible to find at least two sources I and J such that $h(\pi_i, \pi_j) = 1$ , then pessimistic estimation of the number of sources in overall agreement provides m = 1 source. However, $\pi_{(1)}(\omega)$ is no less than the disjunctive fusion described in section 0.18.

If the number of sources p to fuse is 2, then the rule of adaptive fusion (56) is found.

If $h(\pi_1, \pi_2) = 1$ (agreement of the two sources), then m = n = 2 and

$\pi_{\text{adq}}(\omega) = \pi_{(2)}(\omega) = \min(\pi_1(\omega), \pi_2(\omega))$

If $0<h(\pi_1, \pi_2)<1$ (partial conflict), then m = 1 and n = 2, so:

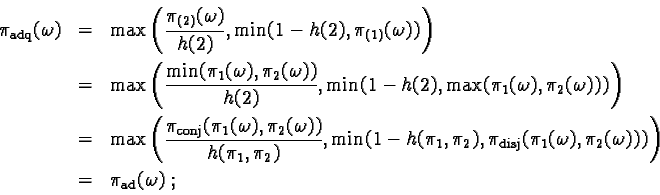$\begin{eqnarray*}\pi_{\text{adq}}(\omega) & = & \max \left( \frac{\pi_{(2)}(\ome...... \pi_2(\omega)) )\right) \\& = & \pi_{\text{ad}}(\omega)~;\end{eqnarray*}$

finally if $h(\pi_1, \pi_2) = 0$ (total conflict), then m = n = 1 and

$\pi_{\text{adq}}(\omega) = \max(\pi_1(\omega),\pi_2(\omega))$

IRIT-UPS