Example

Example

Let us reconsider the problem, posed in the previous pages, of designing a classifier to separate two kinds of marble pieces, Carrara marble and Thassos marble.

Suppose that an observer, watching marble emerge from the mill, finds it so hard to predict what type will emerge next, that the sequence of types of marble appears to be random.

Using decision-theoretic terminology, we say that as each piece of marble emerges, nature is in one or the other of the two possible states: either the marble is Carrara marble, or Thassos marble. We let $\omega$ denote the state of nature, with:

$\omega= \omega_1$ for Carrara,
$\omega= \omega_2$ for Thassos.

Because the state of nature is so unpredictable, we consider $\omega$ to be a random variable.

If the mill produced as much Carrara marble than Thassos marble, we would say that the next piece of marble is equally likely to be Carrara marble or Thassos marble. More generally, we assume that there is some a priori probability P( $\omega_1$ ) that the next piece is Carrara marble, and some a priori probability P( $\omega_2$ ) that the next piece is Thassos marble. These a priori probabilities reflect our prior knowledge of how likely we are to see Carrara marble or Thassos marble before the marble actually appears. P( $\omega_1$ ) and P( $\omega_2$ ) are non negative and sum to one.

Now, if we have to make a decision about the type of marble that will appear next, without being allowed to see it, the only information we are allowed to use is the value of the a priori probabilities. It seems reasonable to use the following decision rule:

$\fbox{Decide $\omega_1$\space if $P(\omega_1)> P(\omega_2)$ ; otherwise decide $\omega_2$ .}$

In this situation, we always make the same decision, even though we know that both types of marble will appear. How well it works depends upon the values of the a priori probabilities:

If $P(\omega_1)$ is very much greater than $P(\omega_2)$ , our decision in favour of $\omega_1$ will be right most of the time.
If $P(\omega_1)= P(\omega_2)$ , we have only a fifty-fifty chance of being right.

In general, the probability of error is the smaller of $P(\omega_1)$ and $P(\omega_2)$ .

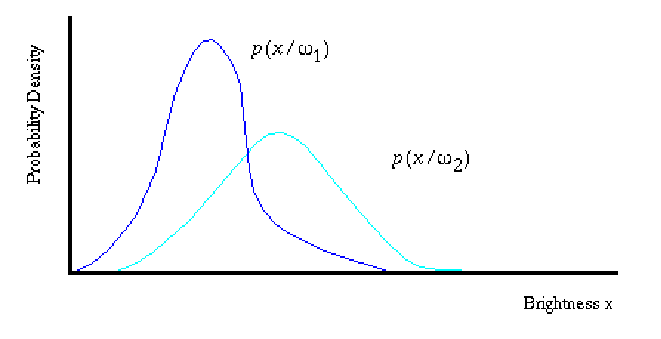
In most circumstances, we have not to make decisions with so little evidence. In our example example, we can use the brightness measurement x as evidence, as Thassos marble is lighter than Carrara marble. Different samples of marble will yield different brightness readings, and it is natural to express this variability in probabilistic terms; we consider x as a continuous random variable whose distribution depends on the state of nature.

Let $p(x/ \omega_j)$ be the state-conditional probability density function for x, i.e. the probability density function for x given that the state of nature is $\omega_j$ . Then, the difference between $p(x/ \omega_1)$ and $p(x/ \omega_2)$ describes the difference in brightness between Carrara and Thassos marble (see figure 16)

**Figure 16:** Hypothetical class-conditional probability density functions.
$\begin{figure}\begin{center}\epsfxsize=14cm\epsfbox{density.ps}\end{center}\end{figure}$

Suppose that we know both the a priori probabilities $P(\omega_j)$ and the conditional densities $p(x/ \omega_j)$ . Suppose further that we measure the brightness of a piece of marble and discover the value of x. How does this measurement influence our attitude concerning the true state of nature? The answer to this question is provided by Bayes' rule:

$\begin{displaymath}p(\omega_j/ x) = \frac{p(x/ \omega_j) \cdot P(\omega_j)}{p(x)}\end{displaymath}$

(3)

where

$\begin{displaymath}p(x) = \sum_{j= 1}^2 p(x/ \omega_j) \cdot P(\omega_j)\end{displaymath}$

(4)

Bayes'rule shows how the observation of value x changes the a priori probability $P(\omega_j)$ into the a posteriori probability $P(\omega_j/ x)$ . Variation of $P(\omega_j/ x)$ with x is illustrated in Figure 17 for the case $P(\omega _1)= \frac {2}{3}$ and $P(\omega _2)= \frac {1}{3}$ .

**Figure 17:** A posteriori probabilities for $P(\omega _1)= \frac {2}{3}$ and $P(\omega _2)= \frac {1}{3}$ .
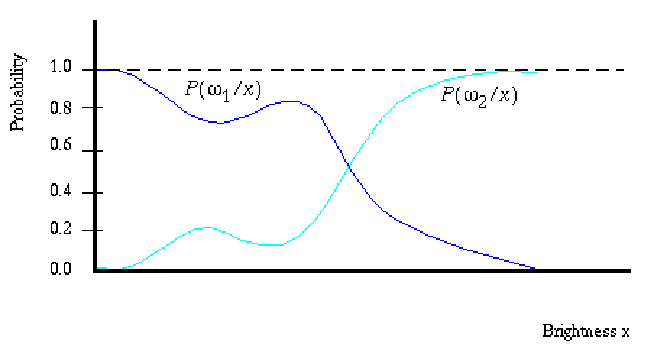
$\begin{figure}\begin{center}\epsfxsize=14cm\epsfbox{posteriori.ps}\end{center}\end{figure}$

If we have an observation x for which $P(\omega_1/ x)$ is greater than $P(\omega_2/ x)$ , we would be naturally inclined to decide that the true state of nature is $\omega_1$ . Similarly, if $P(\omega_2/ x)$ is greater than $P(\omega_1/ x)$ , we would be naturally inclined to choose $\omega_1$ .

To justify this procedure, let us calculate the probability of error whenever we make a decision. Whenever we observe a particular x,

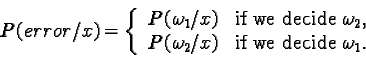
$\begin{displaymath}P(error/ x) =\left\{ \begin{array}{rl}P(\omega_1/ x) & \......2/ x) & \text{if we decide } \omega_1. \\\end{array} \right.\end{displaymath}$

Clearly, in every instance in which we observe the same value for x, we can minimize the probability error by deciding:

$\omega_1$ if $P(\omega_1/ x)> P(\omega_2/ x)$ , and
$\omega_2$ if $P(\omega_2/ x)> P(\omega_1/ x)$ .

Of course, we may never observe exactly the same value of x twice. Will this rule minimize the average probability of error? Yes, because the average probability of error is given by:

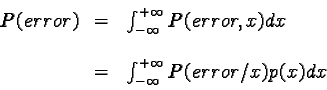
$\begin{displaymath}\begin{array}{rll}P(error) & = & \int_{-\infty}^{+{\infty}}P...... & = & \int_{-\infty}^{+\infty}P(error/ x)p(x)dx\\\end{array}\end{displaymath}$

and if for every x, P(error/ x) is as small as possible, the integral must be as small as possible. Thus, we have justified the following Bayes' decision rule for minimizing the probability of error:

$\fbox{Decide $\omega_1$\space if $P(\omega_1/ x)> P(\omega_2/ x)$ ; otherwise decide $\omega_2$ .}$

This form of the decision rule emphasizes the role of the a posteriori probabilities. By using equation 3, we can express the rule in terms of conditional and a priori probabilities.

Note that p(x) in equation 3 is unimportant as far as making a decision is concerned. It is basically just a scale factor that assures us that $P(\omega_1/ x)+ P(\omega_2/ x)= 1$ . By eliminating this scale factor, we obtain the following completely equivalent decision rule:

$\fbox{Decide $\omega_1$\space if $p(x/ \omega_1)P(\omega_1)> p(x/ \omega_2)P(\omega_2)$ ; otherwise decide $\omega_2$ .}$

Some additional insight can be obtained by considering a few special cases:

if for some x, $p(x/ \omega_1)= p(x/ \omega_2)$ , then that particular observation gives us no information about the state of nature; in this case, the decision hinges entirely on the a priori probabilities.
On the other hand, if $P(\omega_1)= P(\omega_2)$ , then the states of nature are equally likely a priori; in this case the decision is based entirely on $p(x/ \omega_j)$ , the likelihood of $\omega_j$ with respect to x.

In general, both of these factors are important in making a decision, and the Bayes' decision rule combines them to achieve the minimum probability of error.

IRIT-UPS