Implementation of the Bayes' rule

Bayes' Rule Implementation

Our aim is to find, as often as possible, the true class of each pixel. The cost of an error is the same for each error. There is no cost when the class of assignment is the same than the class of membership.

Let T be the matrix of costs whose lines correspond to the true classes and columns with the classes of assignment chosen by the system.

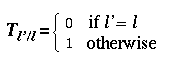(11)

The corresponding matrix of costs is then the following matrix (table 13) :

**Table 13:** Matrix of costs
T	Class of assignment
True class	C₁	C₂	C₃	...	C_q
C₁	0	1	1	...	1
C₂	1	0	1	...	1
C₃	1	1	0	...	1
...	...	...	...	...	...
C_q	1	1	1	...	0

Let us take an example with two classes C₁ and C₂, and three sources of information S₁, S₂ and S₃. The matrix of the probabilities defined by each source S_i for the membership of an object to each class is presented in the table 14.

**Table 14:** Matrix of probabilities attributed by each source for the membership of an object to each class.
P(C_i, d)	Sources
True class	S₁	S₂	S₃
C₁	0.12	0.18	0.30
C₂	0.20	0.16	0.04

For source S₁, it is more probable that

the object belongs to the class C₂ ( P(C₂/S₁) = 0,2)
than to class C₁ ( P(C₁/S₁) = 0,12).

Bayes' rule thus attributes, for source S₁, all the probability with class C₂. Table 15 presents the weights corresponding to the measurements of probability attributed by each source.

**Table 15:** Matrix of weights.
F(l'\|d)	Sources
Class of assignment	S₁	S₂	S₃
C₁	0	1	1
C₂	1	0	0

The probability P(l,l') of having classified the pixel in class l' , whereas its true class of membership is l, is calculated starting from tables 14 and 15 in the following way:

$\begin{displaymath}P(l,l') = \sum_{d \in \mathcal{D}} P(l,d) \cdot f(l'\vert d)\end{displaymath}$

(12)

In our example, the probability P(C₁,C₁) to assign the pixel in the class C₁ which it really belongs is of $(0.12 \times 0) + (0.18 \times 1) + (0.30 \times 1) = 0.48$ .

Moreover, the probability P(C₁,C₂) to be in error by assigning the pixel to the class C₂ whereas it belongs to the class C₁ is $(0.12 \times 1) + (0.18 \times 0) + (0.30 \times 0) = 0.12$ .

In a similar way, P(C₂,C₁)=0.20 and P(C₂,C₂)=0.20 are obtained. These values are included in table 16.

**Table 16:** Errors of assignment.
Errors	Class of assignment
True class	C₁	C₂
C₁	0.12(0)+0.18(1)+0.30(1) = 0.48	0.12(1)+0.18(0)+0.30(0) = 0.12
C₂	0.20(0)+0.16(1)+0.04(1) = 0.20	0.20(1)+0.16(0)+0.04(0) = 0.20

The rule of optimal decision becomes, for a measure d, provided for the pixel in process:

$\begin{displaymath}f(l'\vert d)=0 \text{ si } \sum_{l \in \mathcal{C}} t(l,l') \......in \mathcal{C}} \sum_{l \in \mathcal{C}} t(l,l'') \cdot P(l,d)\end{displaymath}$

(13)

The probability is thus divided between the classes l' which maximize $\sum_{l \in \mathcal{C}} t(l,l') \cdot P(l,d)$ .

IRIT-UPS