| Let us say that we observe patiently a petty-crook cheating
passers by with a die: He places bets that if he throws a die and it comes
out 1, 3 or 5 the passer-by gets a pound, but if it comes up 2, 4 or 6, the
passer-by pays a pound. If we stand and watch for a while, we shall see that
out of the 20 throws, 1 came up only once, 3 twice and 5 once. 2 and 6 came
up five times each and 4 came up six times. Although we may never hold or
study closely the die this petty-crook uses, we may develop a pretty good
idea from these results that this die is loaded. We may even try to model
its behaviour by a function:
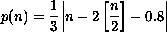
( Here  means integer
part of n divided by 2, i.e. it is 2 if n=5 or n=4, it is 0 if
n=1, etc.) means integer
part of n divided by 2, i.e. it is 2 if n=5 or n=4, it is 0 if
n=1, etc.)
Then if our "friend" asks us to play dice with him, we know that our
prior probability of winning is pretty grim; in fact we may predict
that it is only 20%. The same way we know that the prior probability
of falling from the 10th floor of a block of flats and surviving
is less than 1%. We may not know which die God is going to use if we take
such a plunge, but we may pretty well predict its outcome!

Scientists like to use prior probabilities of events. They usually
calculate them as frequencies of observed outcomes: If you look at the newspapers
and see how many people survived after falling from the 10th floor,
you can calculate the "frequency of survival" as a fraction of the number
of people who survived over the number of all incidents you could find
reported in the newspapers!
In the same way you can predict the prior probability of a hectare
of forest being burned this year if you divide the number of hectares burned
last year by the total number of forested hectares in the world. |