 |




|
|
|
Robustness in linear spectral
unmixing |
| As the whole set of pixels is unmixed simultaneously, one has
to be careful about the reliability of the measurements concerning individual
pixels. For example, if there is a tractor parked in the middle of the field,
the spectral signature of the corresponding mixed pixel will be very different
from that expected. The error term
ei in equation (3) for that pixel will be
very large, and when quantity (5) is being minimised that error will dominate
and influence the chosen values for the mixing proportions of all other
pixels. A more sensible method would try to ignore the influence of such
pixels from the minimisation of the total error function (5). Such methods
are called "robust" methods and rely on the use of "robust
kernels". The kernel used in expression (5) is:
f(eij)=eij2
(6) |
One may use instead:
 |
where t is some threshold value. This is an example of a very simple robust
kernel that selectively ignores the influence of equations that contain very
large error terms. Figure 15 below demonstrates the effect of using robust
kernels to find the least square error line passing through some data points
in 2D: |
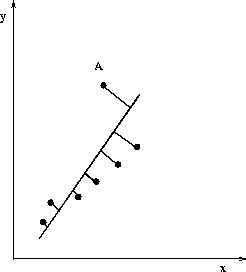
Figure 5a |

Figure 5b |
| The line has been computed so that the sum of the square of the distances
of all the points from it is minimal. |
A better fit is obtained when the "outlier" point A is omitted.
|
 |
|

|