where
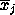 , ,
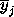 and and
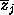 are the mean
reflectances of the three pure classes in band j, and are the mean
reflectances of the three pure classes in band j, and
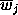 , , and and
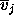 are the mean
reflectances of 3 different mixed sites with mixing proportions,
(a,b), ( are the mean
reflectances of 3 different mixed sites with mixing proportions,
(a,b), (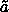 , ,
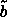 ) and
( ) and
(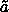 , ,
 ) respectively. If we have
enough regions with known mixing proportions, instead of solving this system
of linear equations in the least square error sense, we can construct an
accumulator array
( ) respectively. If we have
enough regions with known mixing proportions, instead of solving this system
of linear equations in the least square error sense, we can construct an
accumulator array
(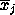 , ,
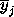 , ,
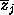 ), so that
along each axis we measure the mean value of a pure class in a specific band.
(Note that we shall have to repeat the process as many times as there are
bands, i.e. we shall have to construct a separate accumulator array for each
band.) For each triplet of regions then we can solve the corresponding system
of 3 equations and identify a triplet of values
( ), so that
along each axis we measure the mean value of a pure class in a specific band.
(Note that we shall have to repeat the process as many times as there are
bands, i.e. we shall have to construct a separate accumulator array for each
band.) For each triplet of regions then we can solve the corresponding system
of 3 equations and identify a triplet of values
(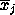 , ,
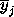 , ,
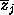 ) which identifies
a cell in the accumulator array, the value of which is incremented by 1.
This is repeated for all triplets of regions we have. The cell of the accumulator
array that has the maximum value at the end, identifies the best mean values
for the pure classes for band j. ) which identifies
a cell in the accumulator array, the value of which is incremented by 1.
This is repeated for all triplets of regions we have. The cell of the accumulator
array that has the maximum value at the end, identifies the best mean values
for the pure classes for band j.
A similar process will yield the best values of the pure classes in any other
band. In a similar way, we may estimate the best values of the elements of
the covariance matrices of the pure classes. We shall have to construct a
separate accumulator array for each element of the covariance matrix. |