| Κλασματικό (fractal) σύνολο είναι εξ'ορισμού ένα σύνολο για το οποίο η διάσταση Hausdorff - Besicovitch ξεπερνά την τοπολογική διάσταση. Mandelbrot (1982) |
| Κλασματικό (fractal) είναι ένα σχήμα
όταν αποτελείται από μέρη όμοια προς το
όλο. Mandelbrot (1986) |
![]()
Παρουσιάζεται μια εφαρμογή των Fractals στην βραχομηχανική περιγραφή της τραχύτητας των ασυνεχειών.
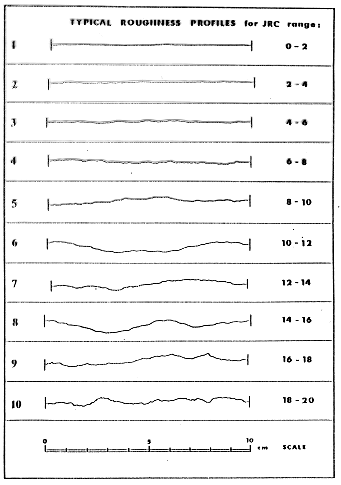
Κλασσική περιγραφή της τραχύτητας των
ασυνεχειών κατά Barton. Σχηματικός πίνακας των
"προφίλ" των ασυνεχειών και της τιμής
τραχύτητας JRC.
Η τραχύτητα των ασυνεχειών μπορεί να εκτιμηθεί με την βοήθεια της κλασματικής διάστασης, με σχέσεις όπως:
|
D = 1 + (0.000534 JRC) JRC = 1870 (D -
1)
[N.H. Maerz, J.A. Franklin] | |
|
JRC = -0.87804 + 2518.96 * ( D - 1 ) - 75246.22 * ( D - 1 ) [Y.H. Lee, J.R. Carr, D.J. Barr, C.J. Haas] |
Στον παρακάτω πίνακα παρουσιάζεται η συσχέτιση του JRC με την κλασματική διάσταση
| Τιμές JRC |
Κλασματική Διάσταση D |
||
| Sakellariou et al. | Lee et al. | Maerz and Franklin | |
| 0 - 2 | 1.0003 | 1.0005 | |
| 2 - 4 | 1.0009 | 1.0017 | |
| 4 - 6 | 1.0013 | 1.0028 | 1.0029 |
| 6 - 8 | 1.0032 | 1.0039 | |
| 8 - 10 | 1.0032 | 1.0044 | |
| 10 - 12 | 1.0042 | 1.0056 | |
| 12 - 14 | 1.0059 | 1.0071 | |
| 14 - 16 | 1.0081 | 1.0081 | |
| 16 - 18 | 1.0074 | 1.0096 | |
| 18 - 20 | 1.0123 | 1.0134 | 1.017 |