 |
 |
![]()
![]()
In Boolean logic, with the rule ``IF X is A THEN Y is B'', the proposition X is A has to be observed to consider the proposition Y is B.
In fuzzy logic, a proposition ``X
is ![]() '', close to the premise ``X is A'' can be observed
to provide a conclusion ``Y is
'', close to the premise ``X is A'' can be observed
to provide a conclusion ``Y is ![]() '' close to the conclusion ``Y is B '' [7].
'' close to the conclusion ``Y is B '' [7].
A simple fuzzy inference can be represented as:
| Rule | : IF | X is A THEN | Y is B | |
| Fact | : | X is |
||
| Conclusion | : | Y is |
To infer such a fuzzy inference we use a mechanism called generalized modus ponens. Here, we use one based on the fuzzy implication of Brouwer-Gödel [6] expressed by:
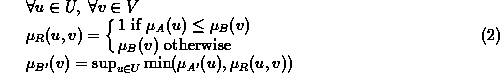 |
Remark: Assume ![]() the operator of the implication of Brouwer-Gödel and
the operator of the implication of Brouwer-Gödel and ![]() the combination operator, the formula (2)
can be expressed by
the combination operator, the formula (2)
can be expressed by ![]() that we use now to simplify notations.
that we use now to simplify notations.