 |
 |
![]()
Edge Detection
![]()
Edge detection locates steep changes of radiometry in the images. A lineament can be detected by means of such a method, because it has two parallel edges.
The transition is highlighted by calculating the first local derivative for a given point, for example with a ``Gradient'' filter.
The models for a lineament are either a profile of ``roof'' type, or a profile of ``valley'' type.
The direction of the edges can be deduced from the horizontal and vertical derivative.
The second derivative, computed for example by means of a ``Laplacian'' filter, often constitutes useful information, because it makes the detection of the edges symmetrical.
The following figures show derivatives on a profile of ``roof'' type.
| Figure 1: Profile of a line | 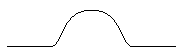 |
| Figure 2: First derivative | 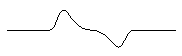 |
| Figure 3: Second derivative | 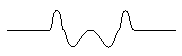 |
The extraction of roads and thin rivers, typically lower or equal to 3 pixels broad, can be done by means of filters of line extraction. This implies that contrast between the lineaments and their environment is sufficient to discriminate them. The principal disadvantage of these detectors is their sensitivity to noise. The process of derivation increases the noise and tends to degrade the images.
Another means of highlighting the edges of the forms is to calculate the morphological gradient, which results from mathematical morphology. The gradient is given by the difference between the dilated image and the eroded image. Such a process transforms a fine line into two parallel lineaments located on the edges of original line. The advantage of this method on the traditional filters, such as SOBEL, is to be independent of the gradient direction.
HO and HONISHI [K.H.L. Ho, 1995a] carry out the edge detection per comparison with simple models, by using concepts of fuzzy logic. Because of the need for fuzzy logic, the image is normalized so that the values of the pixels lie between 0 and 1. The image is then convoluted by the models which constitute masks. The result of this convolution is an image coding the possibility for each pixel of being member or not of a contour. The quality of the result strongly depends on the number of models used, but a great number of models slows down the process considerably.
This is due to the fact that their method does not generalize sufficiently the models, as make it, for example, the fuzzy neural systems. Quality is after all very correct when edges are well contrasted, even if the number of models is restricted. Moreover, the implementation of such a method is simple. The adaptation to the detection of other profiles, lines for example, is immediate, by changing the model set.
NEVATIA and BABU [R. Nevatia, 1980] use a technique based on masks. They use 6 masks 5x5, representing segments of oriented edges, the orientations vary by steps of 30o . The advantage of this technique is to provide a local orientation. This information is used then to carry out a chaining and a polygonal approximation. This technique was the subject of many applications in the field of remote sensing.