The principal problem in edge detection is the noise inherent in the remote sensing images. The more simple way to highlight an edge is to consider a change of radiometry and thus, as seen previously, to locate a significant value of derivative. Noise disturbs the process of derivation considerably, because its effects are amplified, and the result is even more disturbed by false detections.

It is imperative to carry out a preliminary filtering of the image.

Most filters work on a window of small size, and the randomness of the noise is all the more delicate to control that the window is small. Preliminary filtering is thus more effective if a great number of pixels is taken into account. Filtering proposed by MARR and HILDRETH, by means of Gaussian filters of big size solves this problem. In return, the difficulty of localization of edge grows with the size of filters.

Moreover, in practice, one uses filters of limited size, which introduces an effect of cut at the boundaries of the filter and adds noise. Thus, there is a contradiction between

• the effect of filtering, which requires to extend the filter window, and
• the effect of bad localization, which asks to reduce the filter window. (see Figure 4).

The idea of SHEN and CASTAN [J. Shen, 1992] [J. Shen, 1993b] is to use a filter of infinite size, to control the effects of the noise as well as possible, with a " sharp " profile in its center, to improve the precision of localization. They show that the response of their filter is optimal and gives better results that most of traditional methods. The normalized expression of ISEF is given by:

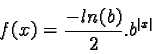
B is the smoothing coefficient.

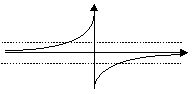
The compared representation of a Gaussian filter and ISEF, and of their first derivative gives:

	Narrow Gaussian	Wide Gaussian	I.S.E.F.
Filter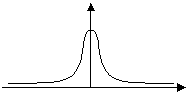
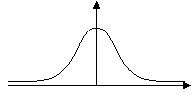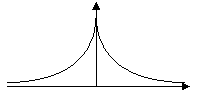First Derivative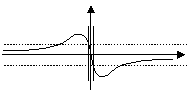
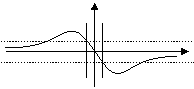Localization Error	Weak	Important	No error

                  
  
 IRIT-UPS