The positioning of the edge point is located at the zero crossing of the first derivative of the filter. For a given threshold, the error of localization is a function of the slope of the first derivative in the neighbourhood of zero. In the case of a Gaussian, the error is all the more significant since the Gaussian is broad. For ISEF, the error is null whatever the extent of the filter, because of the discontinuity at the center of the filter.

For various reasons, and in particular in the aim of simplification, filtering and detection are carried out at the same step. Being given that the derivative of convolution of a image by a filter is equivalent with convolution of image by the derivative of filter, it is possible to carry out them both during the same step.

Detection can be based on two criteria:

• either an extremum of the first derivative, or
• a zero crossing of the second derivative.

First derivative is less sensitive to noise than the second derivative, but can give badly connected edges, due to a bad choice of the selection threshold.

Second derivative, more sensitive to noise, gives many zero crossings but also better connected edges. Taking into account those two criteria makes it possible to discard many wrong detections.

The coincidence of an extremum of the first derivative with one zero crossing of the second derivative provides best edges. This remark is very interesting, because ISEF provides a precise localization of these two characteristics. The following figure 5 illustrates this note:

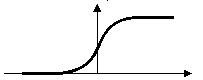
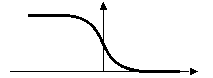
Edge	Positive Edge	Negative Edge
First Derivative
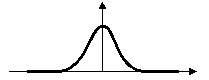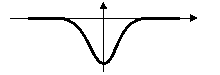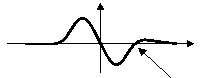
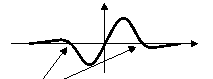
Second Derivative	Wrong edge	Wrong edges

The filter can be extended to the detection of lines [J. Shen, 1993a] by combining

• a detection of zero crossing of the first derivative with
• a thresholding of the second derivative.

In this case also, ISEF filter shows optimal characteristics.