Optimistic and pessimistic estimation of the number of reliable sources

Optimistic and Pessimistic Estimation
of the Number of Reliable Sources

Let p be the number of classes and k the number of sources of information. The principle of quantified adaptive fusion consists in estimating the number of sources in agreement, among k available sources. This estimate is carried out by means of the degree h of consensus between the sources for a given pixel x:

$\begin{displaymath}h(\pi_1(x), \pi_2(x), \dots, \pi_k(x)) =\max_{c=1,p} (\min(\pi_1^c(x), \pi_2^c(x), \dots, \pi_k^c(x)))\end{displaymath}$

(64)

The number of reliable sources is limited by a pessimistic estimate m and by an optimistic estimate n. Let J be any subset of sources. The estimates m and n of the number of reliable sources are obtained by:

$\displaystyle m = \sup \{ \vert J\vert, h(J) = 1 \}$		$\displaystyle \text{(pessimistic estimation)}$	(65)
$\displaystyle n = \sup \{ \vert J\vert, h(J) > 0 \}$		$\displaystyle \text{(optimistic estimation)}$	(66)

As we estimate the number of reliable sources for one pixel at once, the rule of quantified adaptive fusion becomes:

$\begin{displaymath}\forall c \in [1,p] \quad\pi_{\text{adq}}^c(x) =\max \left......{\text{D}}{\underbrace{\min( 1-h(n), \pi_{(m)}^c(x))}} \right)\end{displaymath}$

(67)

The degree of consensus h(n) is obtained by sorting in decreasing order the measures of possibility of membership allotted by each source for a given pixel in a given class c.

Optimistic estimation n of the number of reliable sources is the rank n for which $\pi_{(n)}^c(x) > 0$ while $\pi_{(n+1)}^c(x) = 0$ , and such that $\forall l \in [c+1,p]~; \pi_{(n)}^l(x) < \pi_{(n)}^c(x)$ .
In the same way, pessimistic estimation m of the number of reliable sources is the rank m for which $\pi_{(m)}^c(x)=1$ and $\pi_{(m+1)}^c(x)<1$ , and such that $\forall l \in [c+1,p]~; \pi_{(m)}^l(x) < \pi_{(m)}^c(x)$ .

**Table 32:** Example of possibility measures sorted by decreasing order for a given pixel x.
	S₁	S₂	S₃	S₄
C₁	0.7	0.4	0.2	0.0
C₂	1.0	0.5	0.1	0.0
C₃	0.4	0.1	0.0	0.0

For a pixel x given, after having sorted measurements of possibility by descending order, the calculation of the estimates m and n of the number of reliable sources is carried out by:

$\textstyle m = \max_{c=1,p}(m'_c) \quad$

with $\displaystyle \text{ avec } m'_c = \sup \{ \vert J\vert, h(J) = 1 \}$

(68)

$\textstyle n = \max_{c=1,p}(n'_c) \quad$

with $\displaystyle \text{ avec } n'_c = \sup \{ \vert J\vert, h(J) > 0 \}$

(69)

Table 32 gives an example where the number of reliable sources over a set of four sources must be fixed. Measurements of possibility were already sorted by descending order for each class.

The optimistic estimate n of the number of reliable sources gives

n=3 sources for classes 1 and 2, and
n=2 sources for class 3.

In order to treat all the classes in the same way, we fix n at 3, the greatest possible value.

In the same way for the pessimistic estimate m, the number of reliable sources is

m=1 for class 2, and
m=0 for classes 1 and 3.

We choose to fix m at 1.

The modified rule for adaptive quantified fusion is therefore the following:

$\begin{displaymath}\pi_{\text{adq}}^c(x) =\max \left( \overset{\text{C}}{\over......{\text{D}}{\underbrace{\min( 1-h(n), \pi_{(m)}^c(x))}} \right)\end{displaymath}$

(70)

However there is a class c for which $\pi_{(n)}^c(x) > 0$ and such as for all the other classes $l \neq C, \pi_{(n)}^l(x) \leqslant \pi_{(n)}^c(x)$ . Moreover, $h(n)=\pi_{(n)}^c(x)$ . Therefore 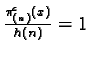$\frac{\pi_{(n)}^c(x)}{h(n) } = 1$ for this class c. In fact, only the part C of the rule 70 is useful.

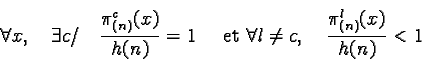
$\begin{displaymath}\forall x, \quad \exists c / \quad \frac{\pi_{(n)}^c(x)}{h(n)......{ et } \forall l \neq c, \quad \frac{\pi_{(n)}^l(x)}{h(n)} < 1\end{displaymath}$

Part D of the rule is useless since part C gives all the possibility for a class c. It is that class which will be selected.

The rule of quantified adaptive fusion, with the restrictions of calculation of the estimations m and n of the number of reliable sources, carried out locally on each pixel, but globally for all the classes, is reduced to the choice of the class having the support of the maximum of sources (optimistic estimate n):

$\begin{displaymath}\pi_{\text{adq}}(x) = \max_{c=1,p}(\pi_{(n)}^c (x))\end{displaymath}$

(71)

We thus came down to an operator OWA of Yager [Yager, 1988]. Let us remind that these operators OWA allot weights w_i to each element to be aggregated. These weights are such as 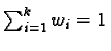$\sum_{i=1}^k w_i = 1$ . The measures $\pi^c(x)$ must be sorted by decreasing order, and the operators OWA carry out the following aggregation:

$\begin{displaymath}\pi_{\text{OWA}}^c(x) = \sum_{i=1}^p w_i \cdot \pi_i^c(x) \end{displaymath}$

(72)

The quantified adaptive rule that we modified (71) corresponds finally to an operator OWA for which w_n=1 and $w_j=0 \quad \forall J \neq n$ . It differs from the operator OWA in the number n of sources which are at least a little in agreement.

This value is calculated for each pixel in order to take into account the degree of coherence of the information available by pixel. This fusion is thus adaptive.

IRIT-UPS