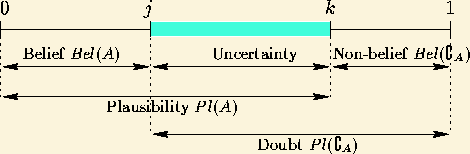Properties

Properties

**Figure 43:** Functions of belief and plausibility.
$\begin{figure}\begin{center}\epsfbox{c3-bel-pl-eng.eps}\end{center}\end{figure}$

[Haralick and Shapiro, 1993b] represent these various measurements over the interval unit (see figure 43).

Let j and k be two elements of [0,1] such that $j \leqslant k$ . We are interested in the interval of belief describing event A:

The interval [0,j] represents the belief Bel(A) in event A.
[k,1] is the non-belief in X, i.e. the degree with which we believe in the negation of A, that is $Bel(\complement_A)$ .
Finally, between these two extremes, is the interval X which represents our uncertainty on the occurrence of event A. This means that we cannot choose between A and the negation of A.

As new information becomes added to what we knew till now, the part assigned to uncertainty decreases being distributed either towards Bel(A), i.e. the belief in event A, or to $Bel(\complement_A)$ , i.e. the non-belief in A. The more information there is, the more uncertainty decreases.

This leads us to the measurement of plausibility Pl(A) of event A which is the sum of the belief Bel(A) in the occurrence of A and of uncertainty on A. This means that the maximum extension possible for belief in A lies in all the belief which does not disprove A.

In the same way, the doubt about the occurrence of A, corresponds to the part of the belief assigned to the negation of A plus the uncertainty related to the occurrence of A.

Belief functions and plausibility functions satisfy:

$Bel(A) \leqslant Pl(A)$

$Pl(A) = 1-Bel(\complement_A)$

$Bel(A) + Bel(\complement_A) \leqslant 1$

$Pl(A) + Pl(\complement_A) \geqslant 1$

Union and intersection of subsets satisfy:

$Bel(A_1 \cup A_2 \cup \ldots \cup A_n) \geqslantBel(A_1) + Bel(A_2) + \ldots + Bel(A_n)- Bel(A_1 \cap A_2 \cap \ldots \cap A_n)$

$Pl(A_1 \cup A_2 \cup \ldots \cup A_n) \leqslantPl(A_1) + Pl(A_2) + \ldots + Pl(A_n)- Pl(A \cap A_2 \cap \ldots \cap A_n)$

IRIT-UPS