Calculation of the possibility distributions from the histograms of grey levels.

Calculation of Possibility Distributions from
Histograms of Grey Levels

To be able to handle spectral information relating to each class, we must represent the histograms of grey level according to the model of representation of information chosen i.e. possibility distributions.

Dubois and Prade [Dubois and Prade, 1983] [Dubois and Prade, 1987a] propose to calculate a possibility distribution from a statistical distribution.

First of all, it is necessary to calculate the frequency of appearance of each grey level starting from the histograms.

**Figure 10:** Histogram of the grey levels for a class c.
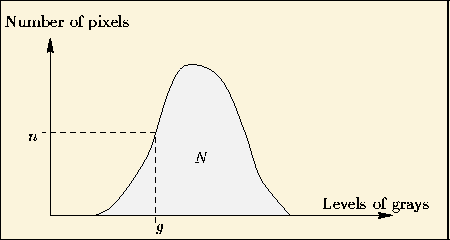$\begin{figure}\begin{center}\epsfbox{c4-histo-vers-proba.eps}\end{center}\end{figure}$

The frequency of appearance f of grey level g for class C_i is obtained by (figure 10) :

$\begin{displaymath}f(g) = \frac{n}{N}\end{displaymath}$

(1)

where:

n is the number of pixels of the samples of class C_i having the same grey level than pixel x,
N is the cardinal of the set of pixels used to built the histogram of class C_i, i.e. the number of pixels located in the samples of class C_i.

The frequency f of appearance of grey level g for class C_i is proportional to the height of the histogram for the grey level of x.

Figure 11: Conversion of a histogram of grey levels into frequencies of appearance, then into possibility distribution (class 3, spectral band MSS4).

Histogram of grey levels

Frequency of appearance

Distribution of possibility

From these frequencies of appearance f(g), possibility measures $\pi^{C_i}(x)$ are then calculated as follows [Dubois and Prade, 1983] [Dubois and Prade, 1987b] :

$\begin{displaymath}\pi^{C_i}(g) = \sum_{f(j) \leqslant f(g)} f(j)\end{displaymath}$

(2)

This transformation gives more weight to radiometries most characteristic of each class (peaks of the histograms, figure 11), but especially brings to the same level these most characteristic radiometries (each class has at least the most characteristic radiometry to which a possibility measure of 1 is set). It finally allows to preserve the general aspect of the histogram.

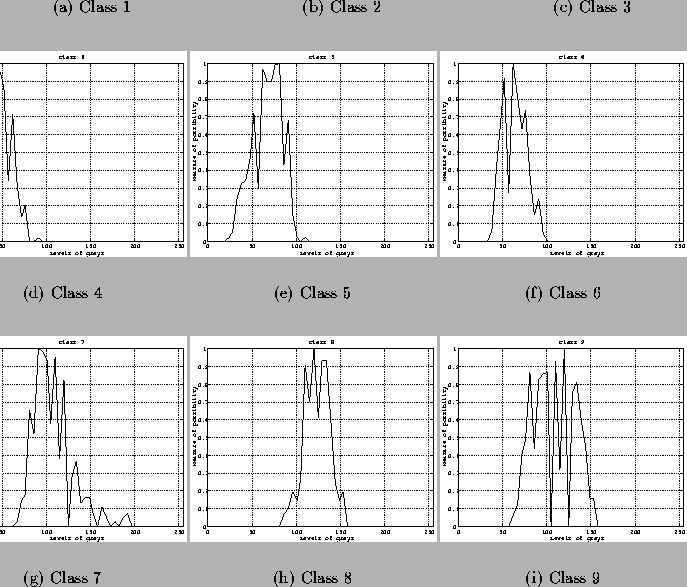
Figure 13 presents the possibility distributions calculated from the histograms in figure 10. These distributions often present a very disturbed aspect because they remained very similar to the original histograms.

A smoothing of those distributions would help in removing the holes present in some distributions. But such a solution has not been used because several classes have already their histograms in a comparable interval of grey levels, therefore strongly merged the ones with the others.

The smooth histograms for these classes should increase their similarities, and thus worsen confusion.

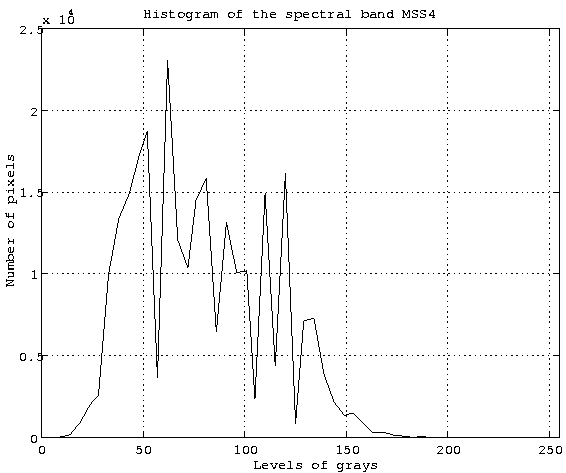
In addition, the histogram for the whole image MSS4 (figure 12) contains holes, due to some grey levels missing. These holes appear also, therefore, in the histograms of the classes.

**Figure 12:** Histogram of spectral band MSS4.
$\begin{figure}\begin{center}\epsfysize=10cm\epsfbox{c4-histo-mss4.eps}\end{center}\end{figure}$

**Figure 13:** Distributions of possibility of each class for spectral band MSS4.
$\begin{figure}\begin{center}\epsfbox{c4-distri-poss-cl1a9.eps}\end{center}\end{figure}$

IRIT-UPS