Intersection of fuzzy subsets: t-norms (triangular norms)

Intersection of Fuzzy Subsets: T-Norms (Triangular Norms)

Let A and B be two fuzzy sets. The degree of membership degree of membership of x to set A is noted $\mu_A(x)$ .

A brief description of fuzzy sets can be found in the previous sections previous pages. For a more complete description of fuzzy sets, refer to the following documents: [Bouchon-Meunier, 1995] or [Zadeh, 1965].

The intersection i of two fuzzy sets A and B is defined by a binary operation over the unit interval (figure 22(b)).

$\textstyle i : [0,1] \times [0,1] \rightarrow [0,1]$

(25)

$\textstyle \forall x \in \Omega \;\;\; i[\mu_A(x), \mu_B(x)] = \mu_{A \cap B}(x)$

(26)

A mapping i is a t-norm if and only if it satisfies at least the following conditions: $\forall (a,b,c) \in [0,1]^3$

axiom i₁: closure condition: i(a,1) = a ;
axiom i₂: monotonicity: $b \leqslant c \Rightarrow i(a,b) \leqslant i(a,c)$ ;
axiom i₃: commutativity: i(a,b) = i(b,a);
axiom i₄: associativity: i(a, i(b,c)) = i(i(a,b), c).

Monotonicity and commutativity properties ensure that a decrease of the degree of membership to set A or to set B, will not involve an increase of the degree of membership to the intersection.

Symmetry of the fuzzy intersection is expressed by commutativity.

Finally, the associativity property ensures that the intersection of any number of sets can be performed in any order.

It is often useful to limit the cluster of fuzzy intersections by taking into account additional conditions as follows:

axiom i₅: i is a continuous function;
axiom i₆: sub-idempotency: i(a,a) < a;
axiom i₇: strict monotonicity: a₁ < a₂ et $b_1 < b_2 \Rightarrow i(a_1,b_1) < i(a_2,b_2)$ .

Continuity avoids the situation where a small change in the degree of membership to set A or set B leads to a large change in the degree of membership to $A \cap B$ .

Axiom i₆ deals with degrees of membership to A or to B having the same value a. This axiom expresses that the degree of membership to $A \cap B$ should not exceed the value of a. Axiom i₇ expresses a higher monotonicity than axiom i₂.

The most common t-norms are the following: $\forall (a,b) \in [0,1]^2$

- standard intersection:	$i(a,b) = \min(a,b)$ ;
- algebraic product:	$i(a,b) = a \cdot b$ ;
- limited difference:	$i(a,b) = \max(0, a+b-1)$ ;
- drastic intersection:	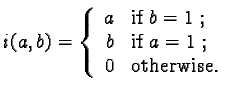$i(a,b) =\left\{ \begin{array}{rl}a & \text{if } b = 1~; \\b & \text{if } a = 1~; \\0 & \text{otherwise.}\end{array} \right.$

$\begin{displaymath}\forall (a,b) \in [0,1]^2, \quadi_{\text{drastic}}(a,b) \leqslant \max(0, a+b-1)\leqslant a \cdot b\leqslant \min(a,b)\end{displaymath}$

IRIT-UPS