If there are no sites fully covered by a single pure class, the statistical
moments of the pure classes have to be inferred. It will be necessary then
to use training data, i.e. data for which we know the mixing proportions
by ground inspection. The set of linear mixing equations then |
will have to be solved for the calculation of
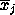 , ,
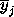 and and
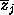 which
are the mean reflectances of the three pure classes in band j. In
(13) which
are the mean reflectances of the three pure classes in band j. In
(13) 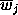 , ,
 and and
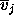 are the mean
reflectances of 3 different mixed sites with mixing proportions,
(a,b), ( are the mean
reflectances of 3 different mixed sites with mixing proportions,
(a,b), (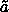 , ,
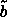 ) and
( ) and
(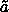 , ,
 ) respectively. The more such
training sites are available, the better the estimates of ) respectively. The more such
training sites are available, the better the estimates of
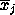 , ,
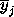 and and
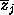 will
be: They will be obtained as the least square error solution of a system
of equations like (13). A similar system of equations will have to be solved
for the elements of the covariance matrices of the pure classes, and so on. will
be: They will be obtained as the least square error solution of a system
of equations like (13). A similar system of equations will have to be solved
for the elements of the covariance matrices of the pure classes, and so on.
|