 |




|
Practical Details |
|
|
Let us say that we have 3 pure classes with spectral values in the j
th band xj, yj and zj
respectively. Let us also assume that we have a mixed region with fractional
cover a, b and 1-a-b from each pure class respectively.
The spectral value of a mixed pixel in the jth band is
wj. From the sets of pure and mixed pixels we have,
we can calculate the mean values of xj,
yj, zj and wj,
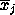 , ,
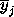 , ,
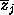 and and
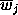 respectively,
as: respectively,
as: |
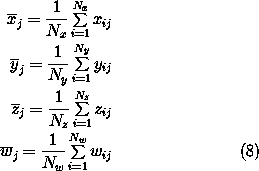 |
where Nx is the number of pixels that represent
the first pure class, xij is the spectral value of the
ith pixel in band j and the meaning of the remaining quantities
is similar. It is known then that the following equation holds between
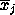 , ,
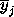 , ,
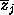 and and
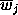 : :
|
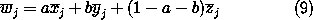 |
| Next, we calculate the elements of the covariance matrix of
each set of pixels, using the following formulae: |
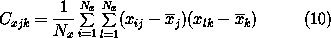 |
| with similar formulae for Cyjk,
Czjk and Cwjk. In the above expression,
Cxjk is the jk element of the covariance matrix
of the x class. From the theory of random variables it is then known
that the following relationship holds between the corresponding elements
between the various covariance matrices: |
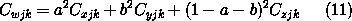 |
| It is possible to calculate 3rd moments for each distribution
and make use of the relationships between them and derive another set of
equations to be used alongside equations (9) and (11). Bosdogianni et.al.
solved the set of equations (9) and (11) in the least square error sense.
They chose values a and b so that the sum of the square of
the errors with which equations (9) and (11) were satisfied was minimum.
However, acknowledging the fact that the mean of a distribution is computed
in a more reliable way than the covariance matrix, they weighted each error
inversely proportionally to the standard error with which each statistic
can be estimated. So, they chose a and b so that the following
expression was minimised: |
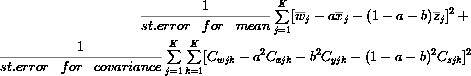
|
|
|
|
|
|
|
 |
What if we do not have data to represent the pure
classes?  |
|
Advantages of the approach
 |
|
Disadvantages of the
approach  |
|
Relationship with the simultaneous unmixing of sets of mixed
pixels  |

|