Angles of gradient vectors

Angles of Gradient Vectors

Initially, the gradient of each pixel of the image is computed. Because of the small size of the rectangles that have to be extracted, the filter used to compute the gradient vector must not smooth too much the image. The Sobel filter gives a good approximation of the gradient without eliminating the smallest rectangles.

The following convolution matrices computes the values of d_x and d_y (coordinates of the gradient vector $\vec{d}$ at point (x,y)):

$\begin{displaymath}M_x= \left[\begin{array}{rrr}-1 & 0 & 1 \\-2 & 0 & 2 \\-1 & 0 & 1 \\\end{array}\right]\end{displaymath}$

$\begin{displaymath}M_y= \left[\begin{array}{rrr}-1 & -2 & -1 \\0 & 0 & 0 \\1 & 2 & 1 \\\end{array}\right]\end{displaymath}$

A rectangle corner forms a right angle, so, for each pixel of the image, the values of the angles $(0 - \Pi/2)$ between the gradient vector of the pixel and each gradient vector of its eight neighbours are computed. Let us consider this angle for pixel p_i and one neighbour p_j:

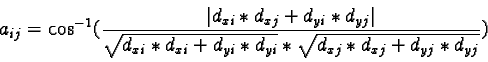$\begin{displaymath}a_{ij}= \cos^{-1}(\frac{\vert d_{xi}* d_{xj}+ d_{yi}* d_{yj}\......_{xi}+ d_{yi}* d_{yi}}* \sqrt{d_{xj}* d_{xj}+ d_{yj}* d_{yj}}})\end{displaymath}$

Where d_xk and d_yk are the coordinates of the gradient vector $\vec{d_k}$ of the pixel p_k.

This angle value and the two norms of gradients d_i and d_j (g_i and g_j) are used to compute a similarity measure with a building corner.

The limit of this similarity measure must be equal to zero when the norm of one of the gradient vectors tends toward zero or when the angle between the two vectors tends toward zero. The maximum of the function is reached when the two gradient vectors are orthogonal and their norms are maximized. BESSETTES and DESACHY propose the following function:

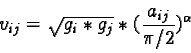$\begin{displaymath}v_{ij}= \sqrt{g_i* g_j}* (\frac{a_{ij}}{\pi/ 2})^\alpha \end{displaymath}$

$\alpha$ is a positive coefficient used to weight the angle participation. If the value of $\alpha$ is close to zero, the value of the angle will have less importance in the calculation of v_ij, whereas if the value of $\alpha$ is very high, v_ij will only have a high value when a_ij is close to $\pi/2$ .

Finally, the pixel is replaced by the mean of the eight values obtained (Figure 62):

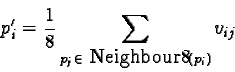$\begin{displaymath}p'_i= \frac{1}{8} \sum_{p_j \in \mbox{ Neighbour8}(p_i)} v_{ij}\end{displaymath}$

Neighbour8(pi) is the set of the eight neighbours of the pixel p_i.

The value of p'_i is very high if the pixel p_i is located at the corner of one or several buildings and so, belong to the urban area.

Each gray level of the resulting image represents the similarity to a building corner.

**Figure 62:** Fuzzy urban mask
$\begin{figure}\begin{center}\epsfysize=10cm\epsfbox{/home/pocquet/LEONARDO/PIERRE/PIERRE3/PRN/fig5.ps}\end{center}\end{figure}$

IRIT-UPS